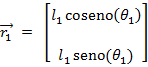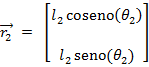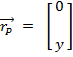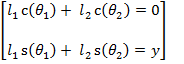|
|
||
|
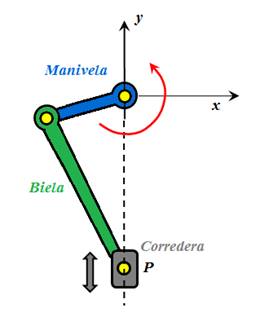
Cinemática del
mecanismo biela-manivela-corredera. |
||
|
Este
tipo de mecanismo se ha utilizado en una gran cantidad de máquinas como un
mecanismo articulado capaz de transformar movimiento circular simple a
movimiento rectilíneo, o viceversa. Se
trata de un mecanismo de un grado de libertad, esto se refiere a que el
movimiento independiente de uno de sus componentes restringe el movimiento de
los demás componentes. En la
figura se ilustra el movimiento de éste tipo de mecanismo para comprimir de
forma automática una bolsa ovalada de un respirador ambulatorio. |
|
|
|
Los elementos que constituyen
este mecanismo simple son la manivela que efectúa un movimiento de rotación
pura, la corredera que efectúa movimiento de traslación lineal y la biela que
efecúa un movimiento combinado de rotación y traslación.
El lector interesado puede
conocer un ejemplo de la aplicación de éste mecanismo en el diseño
de la prótesis de una rodilla. |
||
|
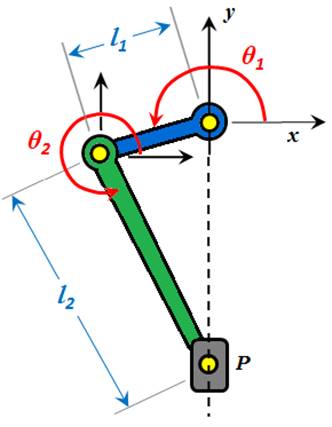
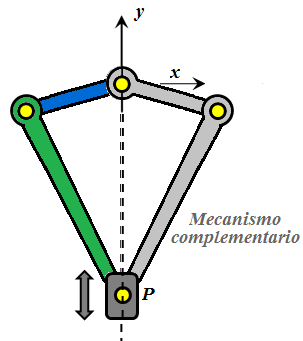
De esta forma, el mecanismo puede ser analizado
considerando los parámetros que se muestran en la siguiente figura |
||
|
|
Siendo: l1
– Longitud efectiva del eslabón 1 (manivela). l2
– Longitud efectiva del eslabón 2 (biela) P
– Posición del punto P (0,y) θ1
– Ángulo del eslabón 1. θ2
– Ángulo del eslabón 2. Los vectores de posición que describen al mecanismo se
pueden representar como:
|
|
|
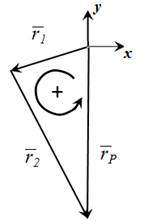
De esta forma, la ecuación general de movimiento del
mecanismo es: r1 + r2
– rp =0 ..(1) Siendo:
Simplificando
|
||
|
Observando el conjunto de ecuaciones se deduce que el
problema cinemático directo se resuelve conociendo la longitud de los
eslabones y cualquiera de los ángulos, de acuerdo a como se ejemplifica en el
simulador. De la primera ecuación de (5) se despeja de forma directa
el ángulo desconocido, y una vez determinados ambos ángulos el valor de “y”
se obtiene por sustitución directa en la segunda ecuación. El problema cinemático inverso se plantea considerando
como datos conocidos la longitud de los eslabones y la coordenada “y”. De
esta forma, dicho problema se resuelve obteniendo los valores de los ángulos
que satisfacen la posición de la coordenada “y”. Precisamente, la cinemática
inversa es en la mayoría de los casos de diseño lo que hay que resolver para
analizar el comportamiento del mecanismo. Existen diversos métodos para obtener su solución como
son el Método gráfico, el método algebraico, o bien aplicando un método
numérico como Newton-Raphson. En este ejemplo, se utilizará el método algebraico. De
las ecuaciones en (5) se procede a despejar el término de
Despejando el ángulo
Y de la primera ecuación en (5)
|
||
|
Con el propósito de evitar inconsistencias o
singularidades en el modelo matemático, es importante reconocer que la
posición máxima del punto P se obtiene cuando |
||
|
A fin de verificar las ecuaciones de posición, se presenta
una simulación java applet, en la cual se ha considerado l1
= 0.21 [m], l2
= 0.35 [m] y una variación de la coordenada y Î (-0.2,-0.4) [m].
|
||
|
Es apreciable reconocer que la ecuación (7) no reconoce la
diferencia entre valores positivos o negativos de la coordenada “y”, por lo
que habrá que considerar el cuadrante en donde se encuentra el ángulo También es importante reconocer que para un mismo valor
de la posición vertical del punto P existen dos soluciones de mecanismos que
satisfacen dicha posición. Queda como
ejercicio plantear y resolver la posición cinemática inversa del mecanismo
complementario. |
|
|
|
Con relación a la velocidad y a la aceleración de los
elementos del mecanismo, es suficiente aplicar la primera derivada total y la
segunda derivada total, respectivamente. Generalmente la variable conocida se
parametriza con respecto al tiempo. Como ejemplo, supongamos que se desea girar de forma
constante
Por lo
que Con relación a la velocidad de
La velocidad de la coordenada “y” queda definida por la derivada
total de la segunda ecuación de (5), resultando:
Las
aceleraciones restantes del mecanismo se obtienen derivando (10) y (11). Queda como ejercicio para el lector
obtener dichas derivadas. |
||